La ecuación por la que empezamos es una igualdad entre una exponencial y un número entero que puede escribirse como una potencia con la misma base que la exponencial.
Por ejemplo, la ecuación puede escribirse como
Teniendo en cuenta que dos potencias con la misma base son iguales si, y solamente si, sus exponentes son iguales, la solución de la ecuación es .
Resolver la ecuación igualando exponentes de potencias con base común:
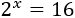
Escribimos 16 en forma de potencia:
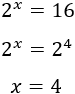
Hemos igualado los exponentes de las potencias porque el resultado de es igual a si, y sólo si, .
A veces, también tendremos que escribir las bases de las exponenciales como potencias. Por ejemplo, en la ecuación
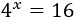
escribimos 16 como la potencia y la base de la exponencial 4^x
como para tener bases comunes:
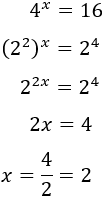
Si tenemos números, potencias o exponenciales que multiplican a las exponenciales, podemos simplificarlas
aplicando las propiedades de las potencias.
Ejercicios para practicar:
El desarrollo de esta actividad, lo podrás ver en:
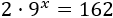
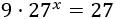
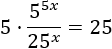
Comentarios
Publicar un comentario